On the second and final part of this conceptual introduction to Machine Learning (ML), I’ll discuss its relationship with other areas (like Data Science) and describe what I perceive as a common theme among many of the ML algorithms. Emphasis on “what I perceive”: don’t take this as the truth.
Models
To a certain extent Machine Learning is about modeling. You are dealing with some domain from the real world, right? It doesn’t matter whether it is healthcare, real-estate or orange farming: you are trying to answer some question or get insights about something real. Unfortunately, we cannot feed the real-world directly to a computer: we need to first convert it to a mathematical model.
Let me return to the made-up orange farming examples from my previous post. We want to predict how many oranges a given orange tree will produce in one season (this is, therefore, a regression problem). Let’s pretend that things are much simpler than they actually are and that we can make a reasonable prediction based only on the height of the tree. Over the years we measured several trees and counted how many oranges each of them produced. This is our training set and here’s a plot of it:

A plot of our training set. We want to predict how many oranges a tree of a certain height will produce.
Luckily, this is an easy case: a straight line passing through the origin will be a reasonably good model for our problem. We still don’t know what is the ideal slope of this straight line, but that’s OK for now. As far as modeling goes, we are done: our model is a straight line passing through the origin, and this model has one parameter which is the line slope.
But wait, did say “luckily”? This was not luck. This was easy because I made up the data and wanted it to be simple. Much more often than not, real problems and real data are much more complex. Things will not be linear. We’ll not have a single independent “input” variable (“tree height”), but hundreds or thousands of them. And the model itself will have much more than a single “slope” parameter (again, thousands of parameters are not uncommon).
Anyway, easy or hard, the point is that ML often starts by modeling: we must transpose the real-world to something a computer can deal with.
Interlude: Machine Learning, Computer Science, Statistics, Data Science…
Before discussing how to determine the slope of our produced oranges × tree height line, let me digress a bit and talk about how Machine Learning relates with other fields.
How do we create models? Certain ML techniques naturally lead to certain models,1 while in other cases we have more freedom to determine how the model is. But in every case, having a good level of familiarity with the data we are dealing with will help.
It is easy to plot graphs in two or even three dimensions to get insights about the data. Now try to imagine how to visualize data for a problem with 1000 or 2000 independent variables. This is where Data Science (another hot buzzword!) comes into scene. Data scientists spend a lot of time analyzing data. They have the knowledge and the tools to get the kind of insights that can be useful when building nontrivial ML systems.
And then, of course, this is all based or influenced by other, more traditional fields. Just to give two obvious examples, there is a lot of Statistics involved, and this is all happening inside computers, so statisticians and computer scientists play important roles here, too.2
I find all this quite stimulating. Yes, the amount of things yet-to-be-learned is daunting, but these increasingly blurred borders between fields are really nice, if you ask me.
End of interlude.
Cost Function
So, we measured our orange trees, counted how many oranges they produced, plotted this data and decided to model this as a straight line passing through the origin. We know that a straight line will not fit the training set perfectly, what would be the slope giving us the best possible fit for the training set?
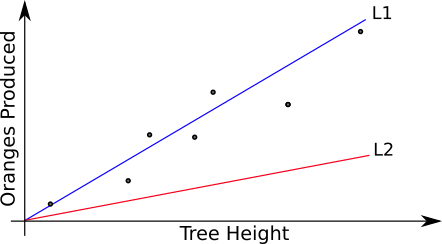
Two straight lines trying to fit the training set. The blue one (L1) does a better job than the red one (L2).
Just looking at the picture above, we intuitively know that the line L1 (in blue) does a better job in fitting our training set than L2 (in red). But just looking at pictures is not good enough for us: we need something that objectively measures how much a certain model and its parameters deviates from perfection.3 The name of such thing is cost function (AKA loss function).
In our example, the cost function could simply be a measurement of the mean difference (or error) between each of the samples in the training set and the value “predicted” by the parameterized model.
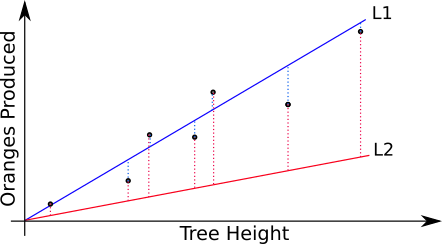
The errors (difference between the prediction and the actual value from the training set) are shown as dotted lines. The dotted lines for the blue line (L1) are, on average, shorter than those for the red line (L2). That’s why we can say that the blue line is a better fit for the training set.
Optimization
Once we have a model with parameters and a cost function, all we have to do is to chose the parameter values so that the cost function is minimized. In other words, we want to optimize our parameters, or adjust them so that the model does the best job it can possibly do. Many of the algorithms use in ML are optimization algorithms used in this step.
For a simple case as in our made-up orange farming example, it is easy to plot the cost (as measured by the cost function) as a function of our one parameter. It would look more or less like this:
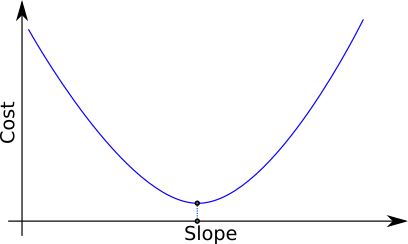
A plot of the cost as a function of our single parameter (the line slope). We want to use the slope that corresponds to the point of the graph with the minimal value.
Again, that’s as easy case. We have one simple minimum, which is relatively easy to find. In practice, we often have local minima, which can complicate the task of finding the optimal parameter value. Sometimes, some of the local minima can be good enough to make our ML system work satisfactorily. Other times, they just cause us headaches.
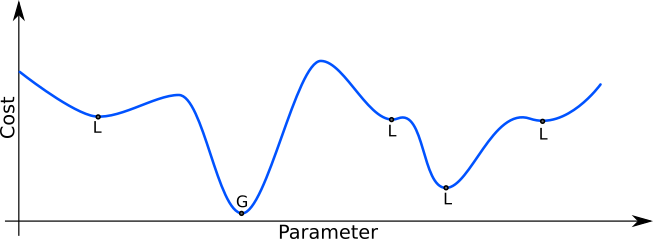
A hypothetical plot of the cost as a function of one parameter. Here, in addition to the global minimum (G), we have some local minima (L) which make the optimization task more difficult.
And then, I have just shown cases in which the model has a single parameter. Recall that real-world problems may have thousands of parameters, which makes the optimization task more challenging. That said, the task is the same: find values for the parameters so that the cost is minimized.
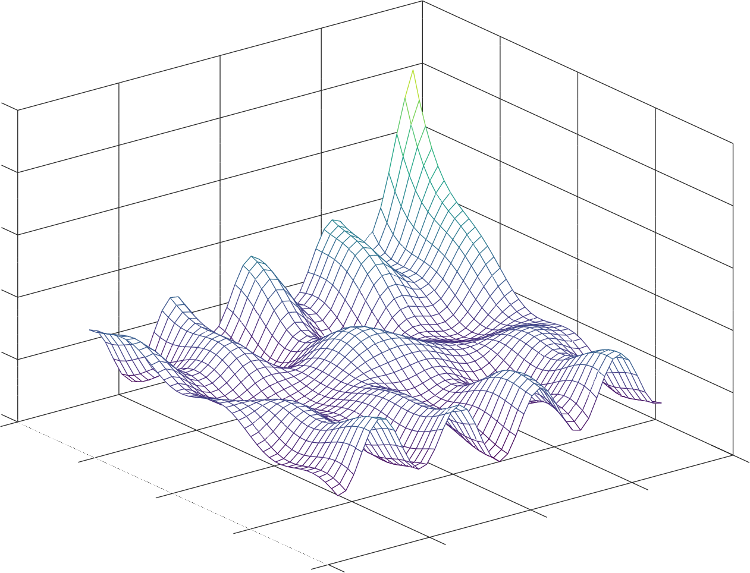
A hypothetical plot of the cost as a function of two parameters. Real-world problems can have thousands of parameters.
Once we have the optimal parameters for the model, we pretty much done: we can use the model along with these parameters to predict how many oranges our trees will produce.
Summary
In summary, two of the main tasks of building a Machine Learning system are creating a model and finding optimal values for the model parameters. There might be exceptions, but these are very common steps. My descriptions and examples were biased towards supervised learning, but even unsupervised learning algorithms will often have these two steps in a form or another.
Of course, these are not the only the tasks necessary to build ML systems. I mentioned, for example, that we often need to spend some time understanding and getting insights about the data in our training set (this is one way in which Statistics and Data Science can be useful for ML), but there are potentially more required tasks, like testing, comparing different models and combining different subsystems so that each one can perform one sub-task in more complex applications.
What’s next?
Right now, I am not planning any specific post about Machine Learning, but I intend to keep looking into the topic. There are three things I plan to do. In no particular order, the first is to try some of the many available tools, languages and libraries used for ML work. Second, I’d like to look deeper at some specific algorithms and learn some I don’t know yet. Third, and very important, I want to actually use ML, get the hands dirty, succeed solving some problems and fail solving others.
I hope to write posts about my next steps, but don’t hold your breath!
-
I don’t want to get into details about specific algorithms here, but here is one concrete example. If you decide to use a Feedforward Neural Network (AKA Multilayer Perceptron or MLP), you get a large part of the model for free. You still have to determine things like the number of layers and the number of neurons in each layer, but the overall structure of your model cannot vary too much. I would probably not be very wrong saying that a Feedforward Neural Network is much a model than anything else. ↩︎
-
In the same paper I quoted in my previous post, Mitchell says that “Machine Learning is a natural outgrowth of the intersection of Computer Science and Statistics.” ↩︎
-
“Perfection” may be a bad choice of words. A “perfect” (and perfectly parameterized) model, as I meant here, would be one that matches exactly the values on our training set. However, a “perfect” match like this is likely to cause problems in practice. ↩︎
